数学や統計学をある程度学び進めていくと必ず出会う世界が微分積分です。
そして、数学・統計学に限らず、物理学、経済学、生物学などあらゆる分野でも、その学問を突き詰めていこうとすると微分積分の知識が必要になる場面が訪れてきます。
微分積分というものが現代社会に大きく貢献していることは何となく理解していても、その中身がどんなものはすっかり忘れてしまっている方は少なくないはずです。
そこで、ここでは「微分法とは何か」という答えを、図解を用いてイメージ化し、難しい数式は使わずに解説していきます。
微分の計算はできるけど、意味はよく分からない。もう一度基礎から学びなおしたい。
そうした方に向けて書いた記事です。
教科書を読むだけ分からないことを図解して説明しますので、微分に対するモヤモヤや苦手意識を吹き飛ばすきっかけになれば幸いです。
微分法につながる「平均変化率」
微分法を学ぶためには「平均変化率」という考え方を理解する必要があります。
そして、この平均変化率という考え方は、日常世界に溶け込んだ考え方でもあるので、まずは構えずに話を聞いてください。
では、日常世界で利用されている平均変化率の一例を挙げてみたいと思います。
それがコチラです。

車を運転しているとこのような道路標識を目にしたことはありませんか。
私が住む田舎町は、坂道だらけなのでこの看板がそこかしこに存在します。(笑)
そうです。この道路標識は「平均変化率」を用いて坂道があることを注意喚起しています。
つまり、この道路標識の中に書いてある『10%』という数値の意味を理解できるあなたは、すでに平均変化率を理解できていることになるわけです。
では、この『10%』の数値の意味を図で表現します。
それが次の図になります。
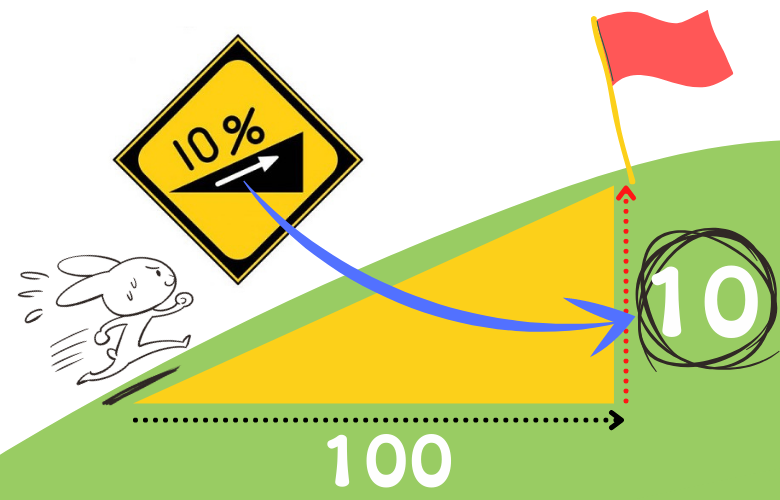
目の前にある坂道において、登りはじめの今いる地点から、登り終わるGOAL地点までを直線で結んでできる辺を斜辺に持つ直角三角形を考えます。
それが、図中に黄色で書いてある三角形になります。
この直角三角形は、底辺の長さが100、高さが10の直角三角形です。
つまり、道路標識内の10%は、底辺に対する高さの割合が10%であることを意味しています。
この道路標識がある坂道は、スタート地点からゴール地点までたどり着くまでに、横に100進む間に上に10登らなければいけない状態にあるわけです。
これで平均変化率の意味はもう完璧に理解できました。
道路標識の数式化
道路標識の意味が分かったところで、平均変化率を数式で表すことにも挑戦してみましょう。
まず第一歩として、坂道の形を関数の世界である座標平面に埋め込んでいきます。
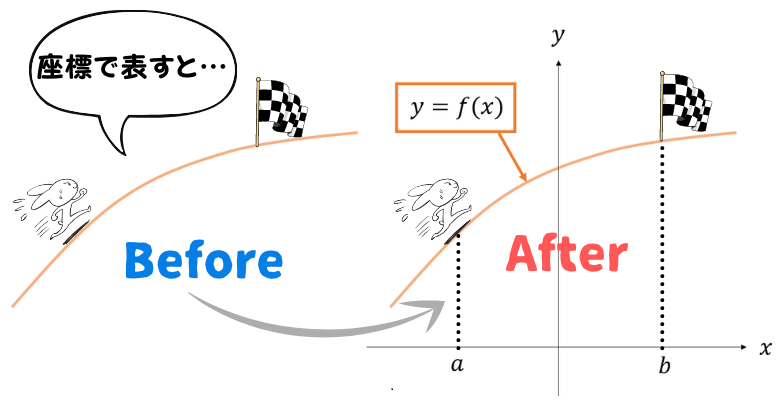
こうすることで、坂道の形は という関数で表すことができるようになります。
この表現について、理解が難しい方は後程具体例で説明しますので、ご安心ください。
次に、坂道を登り始めるスタート地点を とし、坂道が終わるゴール地点を
とします。
こうすることで、
- スタート地点の高さを
- ゴール地点の高さを
と、関数の式にそれぞれの位置情報( の値)から、スタート地点とゴール地点の高さを求めることができるようになります。
道路標識がある坂道の世界を、関数の舞台に当てはめたところで道路標識の中にあった平均変化率『10%』の導き出し方を整理します。
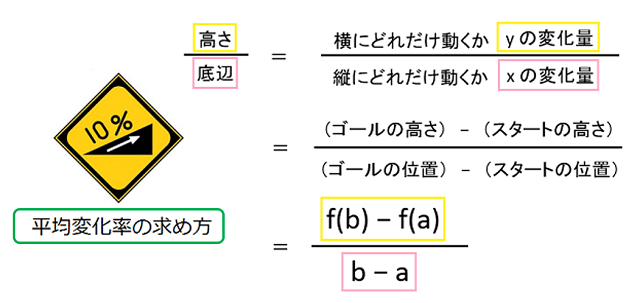
数式化するとどうしても表現が難しくなってしまうのですが、ここで大切なことは、平均変化率は直角三角形の底辺と高さの割合だということを忘れないことです。
上の式化の流れを見て、よく分からなくなってしまった方でも、平均変化率は坂道を上るのがどんだけ大変なのかを数値化したということだけは頭に入れておきましょう。
平均変化率の問題点
平均変化率は坂道の状態を表しており、その数値からどれだけ坂道が上っているのかを理解することができることを説明してきました。
しかし、ここまで説明してきた平均変化率には大きな欠点が存在します。
そして、その欠点を解消するために考えだされた手法が微分法です。
まず平均変化率に潜む欠点について説明します。
平均変化率に潜む欠点は、次の図を見ていただければご理解いただけると思います。
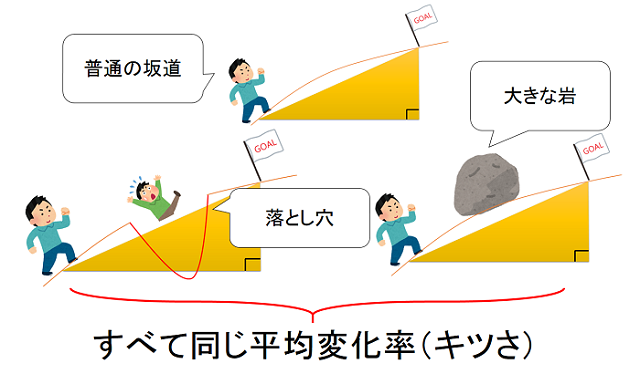
平均変化率を求めるには、スタート地点の情報と、ゴール地点の情報しか使いませんでした。
つまり、スタートとゴールの途中がどうなっていても同じ数値になるわけです。
これこそが、平均変化率の大きな欠点です。
上図のように、大きな落とし穴があるかもしれませんし、大きな岩があるかもしれません。
それでも、何もない普通の坂道と同じ値が出てしまいます。
この問題を解消するために登場する考え方こそが「微分法」です。
平均変化率の問題を解決する「微分係数」
目の前にある坂道がどれほど登るのに大変なのかを数値化するために、スタート地点とゴール地点の情報を用いた指標が平均変化率でした。
平均変化率の計算方法だと途中の情報が抜け落ちてしまう欠点がありました。
そこで途中の情報が抜け落ちないように、「微分係数」は坂道を一歩一歩、距離を取らずに坂道がどうなっているのかを調べていく指標になっています。
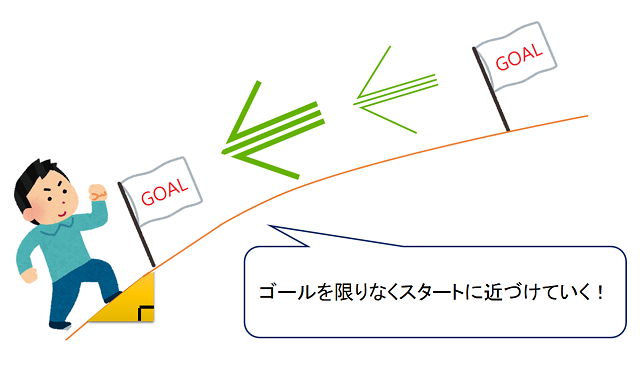
スタートとゴールの距離が離れていると途中の情報が抜け落ち、誤差が生じてしまうのならば、スタートとゴールの位置を限りなく近づけていくことで、一歩一歩(厳密には自分が立っている位置)の状況を数値化していくことを考えていくわけです。
限りなく0に近づけていく

微分という字は「微(かす)かに分ける」と書きます。
スタートとゴールの位置を限りなく細かく刻み、0に近づけていくことを数学では極限という手法で行います。
極限とは という記号を用いて、ゴールをスタートに近づけていきますが、この細かく分けることこそが微分の本質になります。
それでは、使い方も含めて微分係数を求める問題を見ていくことにしましょう。
微分係数の問題例

このままでは分かりにくいため、問題文をかみ砕いてイメージを持つようにしてみましょう。
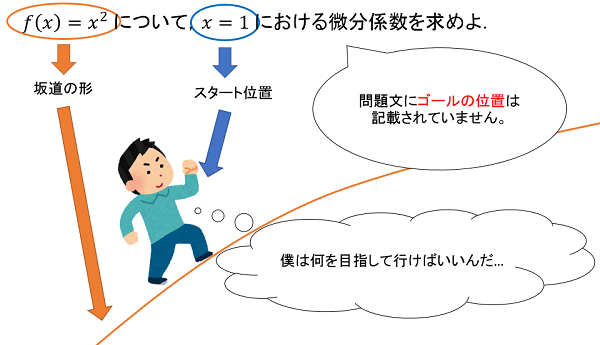
微分係数の問題には、平均変化率の問題と違いゴールの位置が記載されていません。
そこで自分自身でゴールの位置を定めていく必要があります。
自分で定めなければいけないということで不安に思ってしまうかもしれませんが、ゴールの定め方は至って簡単なので安心してください。
ゴール位置は、自分がいるスタート位置から「h」だけ進んだ位置をゴールに設定します。ここで文字「h」が出てくることで難しさを感じてしまうのですが、イメージを大切にしていけば大丈夫です。
まず、ゴールを自分自身でスタート位置から「h」だけ進んだ位置に設定したことで、「平均変化率」を求めることができるようになります。いきなり、微分係数を求めるのではなく、さきほど学んだ平均変化率をまず考えていくわけですね。
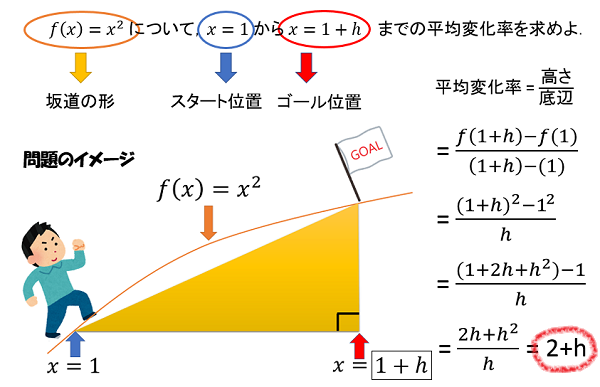
平均変化率の求め方は、(高さ)÷(底辺)でした。三角形の底辺の長さは「h」になり、三角形の高さは(ゴール位置の高さ)-(スタート位置の高さ)で求めることができ、それぞれ坂道の形の式に代入することで得られます。
この計算をすることで、スタート地点 x=1 における平均変化率が 2+h であることが分かりました。
さて、ここでこの平均変化率に潜む問題点を解消するために、ゴールの位置を限りなくスタート位置に近づけていくことで、一歩一歩(厳密には立っている位置)の状況を数値化していきます。
そのために必要なことは、極限をとることでした。この極限の記号を付けることで、スタートからゴールまでの距離「h」はほぼ「0」と考えることができるようになり、それにより平均変化率の問題点を解消し、スタート地点の位置情報を数値化することができるのです。
では、実際にやってみましょう。

極限をとることで、「h」はほぼ0と考えることができるため、2だけが残りこれが微分係数の値になります。
この答えの意味は、スタート地点では「底辺1で高さ2の直角三角形の上に立っている」ことを意味していることになります。
これにより、かなり急激な坂道の途中であることが分かります。
微分係数を一般化したものが「微分」
そして、微分法とは何かですが、微分係数が具体的なスタート位置(上の問題であれば)を扱うのに対し、微分法はスタート位置を一般化し、
のまま考えていく手法になります。
つまり、考え方は微分係数の考え方と一緒なため、微分係数を理解することが微分法とは何かを理解するきっかけになるはずです。
「微分法」の正体
本日は「微分法とは何か」について、できる限り分かりやすい説明を目指してきましたがいかがだったでしょうか。
上の説明の流れをもう一度整理してみると、微分することによりより瞬間的な状況を数値化することができることが分かりました。
限りなく小さく切り分けることで、瞬間的な状況を数値化することができる計算手法が微分というわけです。
物理学で使われる「速度」を微分することで「加速度」が求まる根拠も、ここで紹介した平均変化率から微分係数を求めるまでの流れが理解できれば、納得がいくはずです。
多くの分野に利用される微分法の根本的な考え方に触れることで、解析ソフトで導き出した結果を鵜呑みすることなく検証し、数値を利用できるようになれたら嬉しいですね。
 標準偏差とは何か!その求め方と意味を図解で徹底解説
標準偏差とは何か!その求め方と意味を図解で徹底解説
統計学の知識を分かりやすく解説している「サルでも分かるシリーズ」もぜひ参考にしてみてください。
図解を駆使し、数式を必要最低限に抑えています。数学が苦手な方こそ読んでみてください。


