年収を偏差値で表すと、どんなことが起きるのでしょうか。
「偏差値」という統計量は、受験戦争を通じて日本社会に定着しています。
私も受験期にはこの言葉が大嫌いでした。
受験業界ではもはやなくてはならない統計量になっている偏差値ですが、その数値の高低のみで進学先を決定する風習から偏差値至上主義を生み出し、”悪の元凶”のように目の敵にされてしまっている一面があります。
実際、偏差値に振り回されて嫌な思いをされた方も多いのではないでしょうか。
しかし、これだけ長きに渡り、日本の受験業界に君臨している指標ですから、使い方次第で大きな恩恵を手にできる優れた面も持ち合わせているはずです。
一方で、この偏差値という数値指標は、受験生時ほぼ毎日のように耳にし、その数値を意識して過ごしていきますが、一旦入試を終え、社会に出ると耳にする機会はほとんど無くなります。
社会人になると自分自身の客観的な立ち居地を把握するものさしは、テストの点数から自分自身の収入へと変わっていきます。(もちろんそうではない方も多くいますが)
そんな社会人にとって、ある種唯一とも言える自分自身の数値化された「ものさし」である収入を、受験期に慣れ親しんだ偏差値で表すと、どのようなことが見えてくるのでしょうか。
年収を偏差値化する前に知っておきたいこと
年収を偏差値化する上でいくつか知っておくべきことをいくつか列挙しておきます。
偏差値の定義

偏差値という統計指標は、上の式で計算することができます。
簡単にこの式を説明します。
- 標準偏差 ・・・ データの散らばり
- × 10 ・・・ 散らばりを10区切りにする修正式
- + 50 ・・・ 平均が50になるようにする修正式
標準偏差というデータの散らばり度を数式に組みこみ、扱いやすいデータに加工したものが「偏差値」という統計量になります。
標準偏差というデータの散らばり度を数式に組みこみ、扱いやすいデータに加工したものが「偏差値」という統計量になります。
標準偏差を図解で解説
 標準偏差とは何か!その求め方と意味を図解で徹底解説
標準偏差とは何か!その求め方と意味を図解で徹底解説
こうして定義された偏差値は、次のような性質を持ち合わせることになります。
☒ 偏差値50 ⇒ 平均値
☒ 偏差値40~60 ⇒ 68%が所属
☒ 偏差値61以上 ⇒ 上位15%
☒ 偏差値39以下 ⇒ 下位15%
年収を偏差値化する意義は、上記の「偏差値の性質」を年収に当てはめていくことにあります。
年収を偏差値化する意義
なぜ年収を偏差値化しようと考えたのかというと、年収というデータを代表する数値指標として「平均年収」のみが焦点化されすぎていることに疑問を抱いたからです。
当サイトでは「平均値」という指標を用いていろいろなシミュレーションを行い、これからの時代の生き方や暮らし方について提言しているのですが、こうした分析を行っていると「平均値」という指標がもたらすイメージ像が実感する世界と乖離している感覚を抱くことが多々あります。
平均値の何が問題なのか
 平均的な年収で、平均的な暮らしはできるのか?
平均的な年収で、平均的な暮らしはできるのか?
平均値は確かに便利な代表値ではありますが、そこだけに注視してしまうと、見えるものも見えなくなってしまうのではないでしょうか。
そんな思いから、年収を偏差値化した世界を体感してみることにしました。
年収を偏差値化した世界
ここでは国税庁が発表している民間給与実態統計調査|統計情報|国税庁を用いることで、年収を偏差値化してみたいと思います。
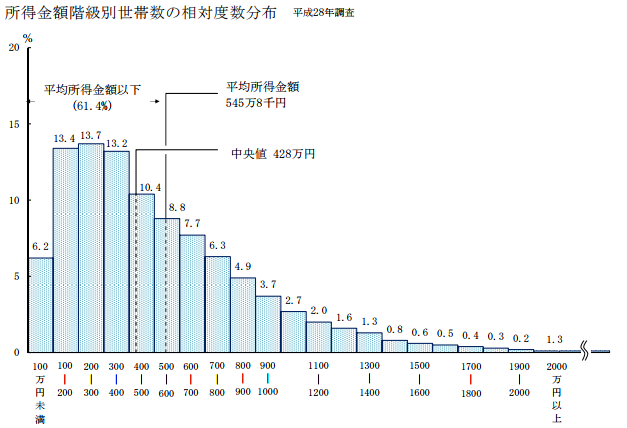
こちらの年収分布をみる限り、正規分布とは程遠い形をしています。
正規分布は試験や身長などのデータを集めた際に見られる左右対称凸形の分布であり、上の年収分布グラフはかなり左側に偏っていることが見て取れるかと思います。
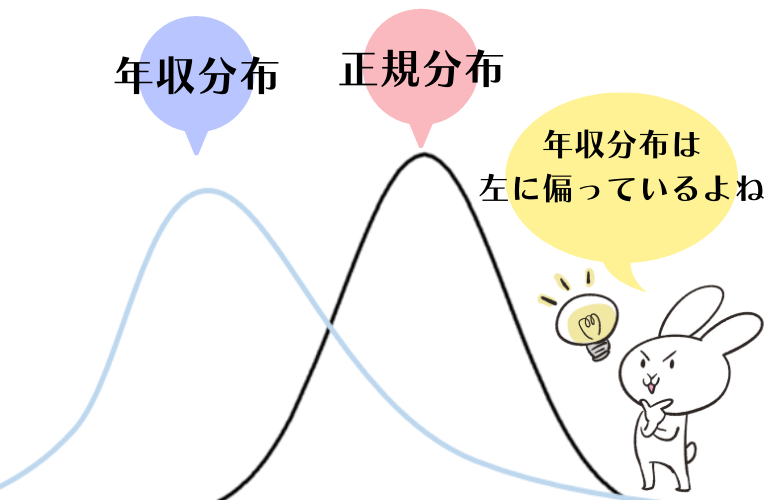
このことが年収を偏差値化する上では大きな問題になります。
年収分布は正規分布と異なり、平均よりも左側(低い年収)に偏っているため、このままでは先ほど紹介した偏差値の性質が当てはまらないのです。
そこで、まず左に偏った形の年収分布を正規分布になるように加工します。
ここでは対数(log)を利用することで正規分布に近付けることに成功したので、その手順を以下で説明します。
年収を対数変換する
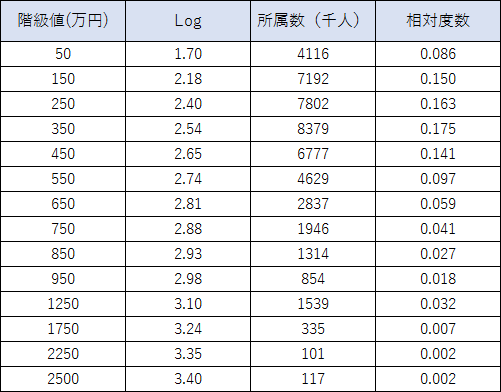
上の表が民間給与実態統計調査をもとに、国民給与所得の階級値に対し対数(log)を取ることで作成した度数分布表になります。
この度数分布表をもとに年収分布が正規分布化されているかチェックします。
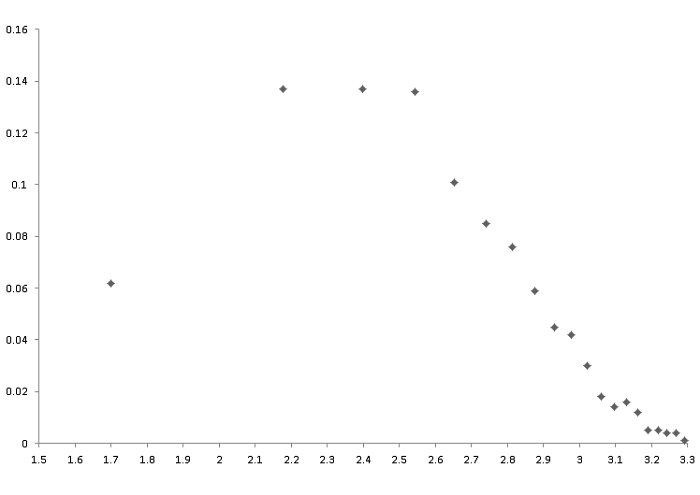
上の階級値の対数(log)と相対度数をプロットした表を見る限り、左側に大きく偏った年収分布が対数(log)を使うことでしっかりと正規分布化されていることが見て取れます。
よかったよかった。
でということで、この数値をもとに計算式に当てはめ、代表的な年収の偏差値を算出しました。
年収を偏差値化してみた
こちらが各年収の偏差値です。
年収500万円で偏差値55を超えてきます。高校生であれば国公立大学が視野に入ってくる優秀な偏差値ですね。
このように平均年収とは違った印象を持つことができるのではないでしょうか。
受験生時代に自分自身の点数の増減で学力を語ることがいかに危険かを学んでいるにもかかわらず、社会人のものさしである年収は増減のみで語られているのが現状です。
テストの点数とは違い、お金は物価指数や金利、為替など多くの指標が複雑に絡み合い、ここで紹介した偏差値化においても客観的指標としては”かなり脆弱”です。
しかし、報道であるような平均値一辺倒の分析では読み取れる情報量がさらに少なくなってしまいます。
標準偏差を考えずに、平均値のみで分析を行うことはゲーム理論でいうところのゼロ・サム(誰かが得したら、誰かが損をする)的な偏った見方になると言われています。
ここで示した年収偏差値を用いることで、平均年収以外の指標として自分自身の年収はもとより、様々な経済状況を分析できるようになるかもしれません。
年収を偏差値化すること見えてくるもの
受験生時代に自分自身の点数の増減で学力を語ることがいかに危険かを学んでいるにもかかわらず、社会人のものさしである年収は増減のみで語られているのが現状です。
テストの点数とは違い、お金は物価指数や金利、為替など多くの指標が複雑に絡み合い、ここで紹介した偏差値化においても客観的指標としては”かなり脆弱”です。
しかし、報道であるような平均値一辺倒の分析では読み取れる情報量がさらに少なくなってしまいます。
標準偏差を考えずに、平均値のみで分析を行うことはゲーム理論でいうところのゼロ・サム(誰かが得したら、誰かが損をする)的な偏った見方になると言われています。
ここで示した年収偏差値を用いることで、平均年収以外の指標として自分自身の年収はもとより、様々な経済状況を分析できるようになるかもしれません。
数字を読み解く力を身に付けよう
年収を偏差値化した世界は、いかがだったでしょうか。
年収を偏差値で表すことの意味は捉え方により様々ですが、今自分自身が置かれている状況を客観的かつ正確に把握することの重要性は誰しもが必要とする情報なはずです。
テストの点数と違い、年収は努力だけではどうにもならない要素があるとはいえ、「だから何もしなくていい」という考え方は、非常に危険です。
平均値や目先の金額の増減だけで語られがちな年収ですが、ここで紹介した年収偏差値を利用することで、より正確な状況分析ができ、新しい目標を定めるきっかけになってくれたら幸いです。
年収偏差値をUPしたい方は…
 公務員から一般企業に転職して年収1000万円になった方法をシェアします
公務員から一般企業に転職して年収1000万円になった方法をシェアします
年収を上げるためにはご自身の転職市場価値を知ることが重要です。
その一歩を踏み出すことで、公務員から年収を大きく上げることに成功した方法を紹介しているのでこちらも参考にしてみてください。



前の記事の「正規分布じゃない云々」コメントに囚われ過ぎてると思うので,見方を変えたアドバイスです.
偏差値の本質って(値-平均)/標準偏差の式ではなくて,むしろ前記事で「偏差値の性質」として紹介されている箇所のように,自分のいまの相対的なポジション(Wikipediaにはパーセンタイル順位と書いています)を知ることです.相対的なポジションを知りたいだけなのに,データが確率分布に当てはまっていないから諦めるというのは本質的な議論ではありません.
データが正規分布に従ってないのなら,逆に「偏差値の性質」を満たすように新しくそのデータの分布に適した偏差値的指標を作ってしまうことを目指すべきです.
新しい指標の作り方はかんたんで,年収分布と正規分布の累積分布を重ねてみることです.
上位15%点で正規分布の偏差値が60なら,年収分布も上位15%の金額で新偏差値を60とします.
年収分布を見たところちょうど上位15%の境界は年収900-1000万円のビンですかね.そこを偏差値60と決めてしまうのです.クラスでちょっと優秀な生徒の位置づけでしょうか.
上位50%で正規分布の偏差値が50なら,年収分布も上位50%の金額(中央値です)で新偏差値を50とします.上にも下にも同数いる,偏差値50の生徒の感覚に近いと思います.
相対的ポジションを50を中心とした指標で測りたい(目的)→(値-平均値)*10 /標準偏差 + 50 を使う(手段)という構造があるのですから,
手段が成り立たない状況では再度目的にたち返って別の手段を導出するといいと思いますよ
えらそうにすみませんでした
なるほど。新しい指標を作ってしまうという発想は全くありませんでした。
箱ひげ図だと四分位数が限界ですが、おっしゃる方法なら細かな相対的ポジションの把握までできるのかもしれませんね。
統計学は奥が深いですね。また、お気付きになったことがあればご教授ください!
初めまして。わたしは62歳の零細開業医です。突然の変なコメントをお許しください。実は、もう10年近く前から新しい経済学を夢想してきました。それは、一言で申し上げると医学生物学的な観点から経済を考えてみたらどうでしょうということです。一時、自然の形状の理解にフラクタル幾何学を用いて説明する手法が流行しましたが、経済も人の活動の産物なので、きっと人体とフラクタルのように関連しているのではないかと思いました。例えば、お金はよく社会という血管を流れる血液に例えられますが、実際に人体に照らし合わせると日銀はお金を送り出す心臓で、家庭や企業は細胞や各臓器、税収や債券は静脈系?という具合。病気の高血圧や低血圧がインフレやデフレのアナロジーにならないか?そうであれば、治療もできるのでは?とか(笑)。実は、収入についてもFuKaSeさんと同じく、対数化をわたしは自然対数でやってみたことがあります。そして、もし医学で用いられる検査値の基準値に当てはめられれば、平均値+2標準偏差(-の方は、低収入なので出ません)を超えている収入のある方は、ある意味「ビョーキ」と言えるのではないかと思いついた次第です。少し前に、トランプ政権の国務副長官だった(?)ピーター・ナバローさんと言う方が、ウォール街の貪欲エリートたちを精神病者扱いしていました。あながち、超金持ちが「ビョーキ」というのは間違ってないのではないかと共感を覚えた次第です。実際、世界の富の90%超をわずか数%の人々が所有し、一方で餓死する人たちが大勢いるのを座視しているのはまともな精神ではない気がします。そこで、さっきの検査の基準値に準じて、基準から外れる収入のある人は、基準値以内になるように治療する、すなわち課税の方法次第で「ビョーキ」を治せるのではないかと思いついた次第です。つまり、わたしの知る限りでは、これまでの歴史で、課税の明確な基準というものは存在してこなかったようですが、収入の正規分布化で人類史上初めて明示されるのではないでしょうか?他にも、感染症ー今回の新型コロナ感染症の広がり方ーとi-Phoneの広がり方を比較したり、国防を免疫の仕組みと対比して免疫に消費されるエネルギーと国防費用を考察したり、など。色々医学生物学的視点から考える経済学というものもありうるのではないかと思います。これまで、どなたか一緒にお考えいただける方はないかとずっと探しておりまして、今回こちらのFuKaSaさんのブログにようやく到達しました。今のところ、バイオロジカルエコノミーという名前で新しい経済学分野を創造できればと妄想しております。厚かましい限りですが、もし面白いとお考えいただければ、ぜひお力添えをお願いできませんでしょうか?なお、わたしは経済学は全く分かりませんので、誰か経済学者の方がアイデアを引き継いでご発表いただければ、それでも幸いです。行動から経済を考えた経済学者がノーベル賞を受賞しています。しかし、行動を起こすのは人体です。その人体を核に経済学を真の意味で経世済民となす学問に近づける。そんなことに一役買えたら素晴らしい余生になります。本当に変なコメントで済みません。何卒ご寛容ください。お騒がせしました。
とても面白い話を聞かせていただき、ありがとうございます。
「医学生物学的視点から考える経済学」という観点はとても興味があります。
もし協力できることがあればぜひぜひお問い合わせボタンからメールを直接いただけたら幸いです。
Fukase様 つい先日メールをお送りしたと思っておりましたら、もう一年経っていました(笑い)。ご親切なお返信を頂いていたのに、大変失礼しました。ご寛容ください。医学生物学的視点から経済を考えるということにご関心をお寄せ頂けたようで、とても嬉しいです。長くいろんなところで披露してきましたが、わたしの経済学や統計学への知識が乏しすぎてうまく説明できませんでした。わたしは、自分の業績にしたいとは露ほどにも考えていませんので、Fukase様が論文や論考におまとめ頂き、適当な所にご発表頂ければと考えます。このブログの中でも結構ですし、例えば雑誌「東洋経済」の「石橋湛山賞」とかどうでしょうか?一番手っ取り早いのは、収入への課税についての考察かなと思います。血液検査で、医者が治療を行うかどうかの判断に、検査値が基準範囲の内か外かという点があります。基準値の線引きは、平均値±2標準偏差、つまり上下2.5%の値を線引きに使います。従って、収入が「ビョーキ」であるかどうかも正規分布から上下の基準値を求められます。治療は、基準域を超えた金額を徴税、基準域を下回る金額を支給することでしょう。これまで、歴史上、徴税についての根拠となる理論は一切ないように思います。ビョーキ理論で可能になるのではないかと思います。ぜひ、ご協力の程よろしくお願い申し上げます。
コメントありがとうございます。
質問についてですが、国勢調査がもとになりますので、15歳以上の所得がある日本人になります。
おっしゃる通り年齢により、数値変動がありますが、年代ごとの統計データが入手できませんでした。
もしいい資料等あればご紹介下さい!
今後もよろしくお願いします。